Ben. Jackie. Brian. John. Meg. The other Ben. Emily. Aunt Karen.
Over the past two months, each of these contestants entered a singularly intense competition to determine, once and for all, who has the deepest understanding of childrens poetry.
It started in 2004, when Will E. Hipson and Saif Mohammad laid down the gauntlet by collecting a dataset of over sixty thousand poems written by children in grades 1-12. Their paper details the ways in which these poems can help us more thoroughly study child language and development. They carefully analyze the emotions present in these poems, for example, in the hopes that that analysis might shed light on arcs of growing up. They look at how those arcs might differ by gender. While not explicitly stated (but if you read closely, strongly implied), their main thesis is not so much an argument but a challenge to fellow researchers: Can you “Guess the Grade”?
Here’s how “Guess the Grade” works: First, pick a random poem in their dataset - for example, the poem “Cats”:
“there are wildcats and bob cats and all sorts of cats ther are tiny cats ther are big cats ther are fat cats there are skiny cats there are furry cats there are silly cats. cats here cats there cats every where, cats, cats, cats, all about cats!”
“Cats” was written by a young author named Aimee. She could be in elementary school, middle school, or high school. The ultimate question is - from Aimee’s poem - can you guess what grade she is in? 1
Ben. Jackie. Brian. John. Meg. The other Ben. Emily. Aunt Karen. All given the same randomly selected subset of 30 poems asked to guess the grade of the author for each. Some have a wealth of relevant experience: Emily is currently studying to be a school counselor, while Aunt Karen was a middle school math teacher for decades and has a PhD in Child and Family Studies. Others maybe less so: Ben studied history and has worked in sales. Time to find out whether that matters.
The first 15 poems
With the first 15 poems came a hard lesson: Guessing the grade is tough. Most people only got 2-3 poems right (Jackie had the most, with 5). But that begs the question: Are all “wrong” answers created equal? Presumably someone who guesses “fifth grade” on a fourth grader’s poem made a better guess than someone who thought the poem was written by a high school senior.
Because of that, the competition was scored based on “Average grades off” - or, in other words, how close an individual’s average guess was. While someone with an “Average grades off” score of 1.5 might not get every grade right, they do tend to make guesses within 1-2 grades of the correct answer.
After the first half, it is clear that some competitors are better suited to this than others.
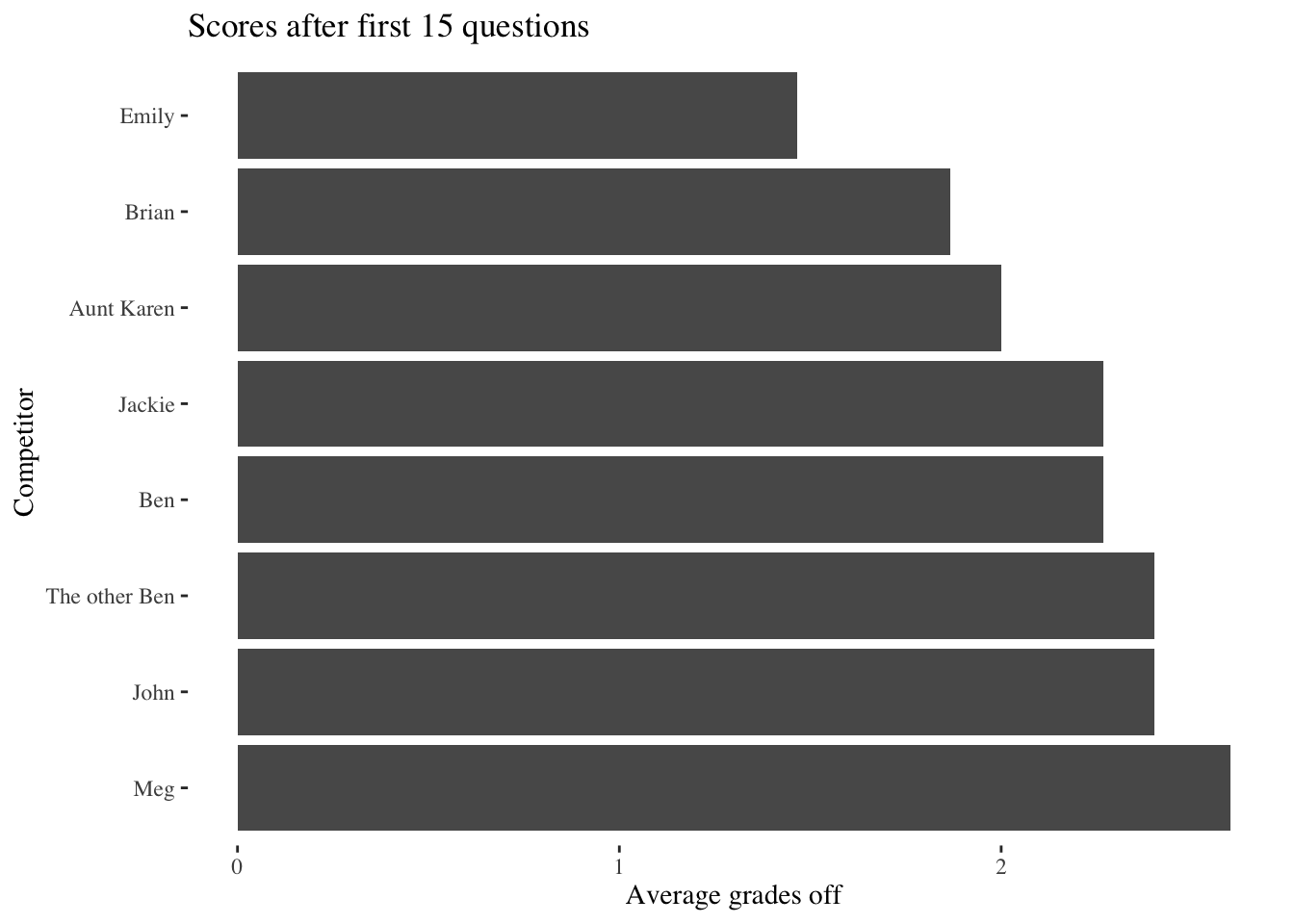
The teacher training pays off! Both Emily and Aunt Karen performed well through the initial 15. Brian - a management consultant with seemingly no relevant skill - starts off strong too. Emily’s guesses in particular were quite impressive.
Compare that to how John performed:
John had a few sizeable misses in “What About?” and “Mad Man” (among others), setting his score back quite a bit.
Maybe most interesting were Jackie’s guesses: As you may recall, Jackie got five poems right on the money - but her other guesses were far enough from the correct answer to make a serious dent in her overall score.
To be fair, “pickels pickels” was a tough one to figure out.
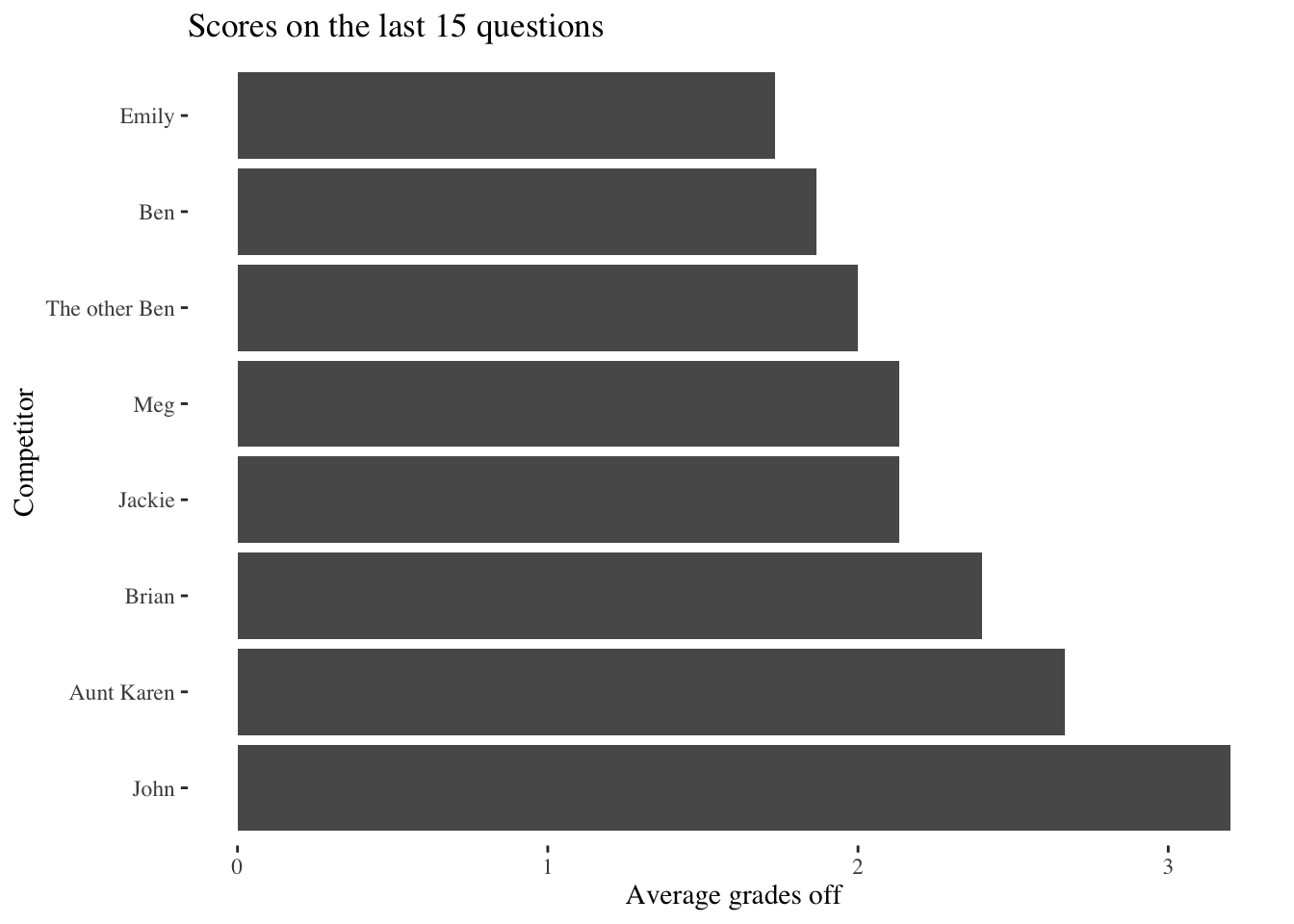
The second half
Emily maintained her lead in the second half while John continued to lag behind. In between, though, there were a number of shake-ups.
Having looked across all 30 poems by this point, it is clear that some poems were universally easier to guess than others. Take, for instance, “Right at….” and “What About?”. While nearly everyone knew that “Right at….” was written by a younger student, “What About?” was harder to nail down.
For the record, “Right At….” was written by a second grader, whereas “What About?” was a fifth grader’s work.
“Right At….” is closer to the exception than the rule. By and large, few poems saw any sort of consensus guess. You can see that in the plot below, which charts up all of the guesses for each poem (red dots represent the correct answer). Once again: Guessing the grade is hard.
Make sure to note that nearly everyone correctly guessed that “Blueberrys” was written by a young elementary schooler, with one lone dissenter convinced that the author of “berries berries you are good you are good for the body and you are blue that is why i like you” was a High School Junior.
So where does this leave us?
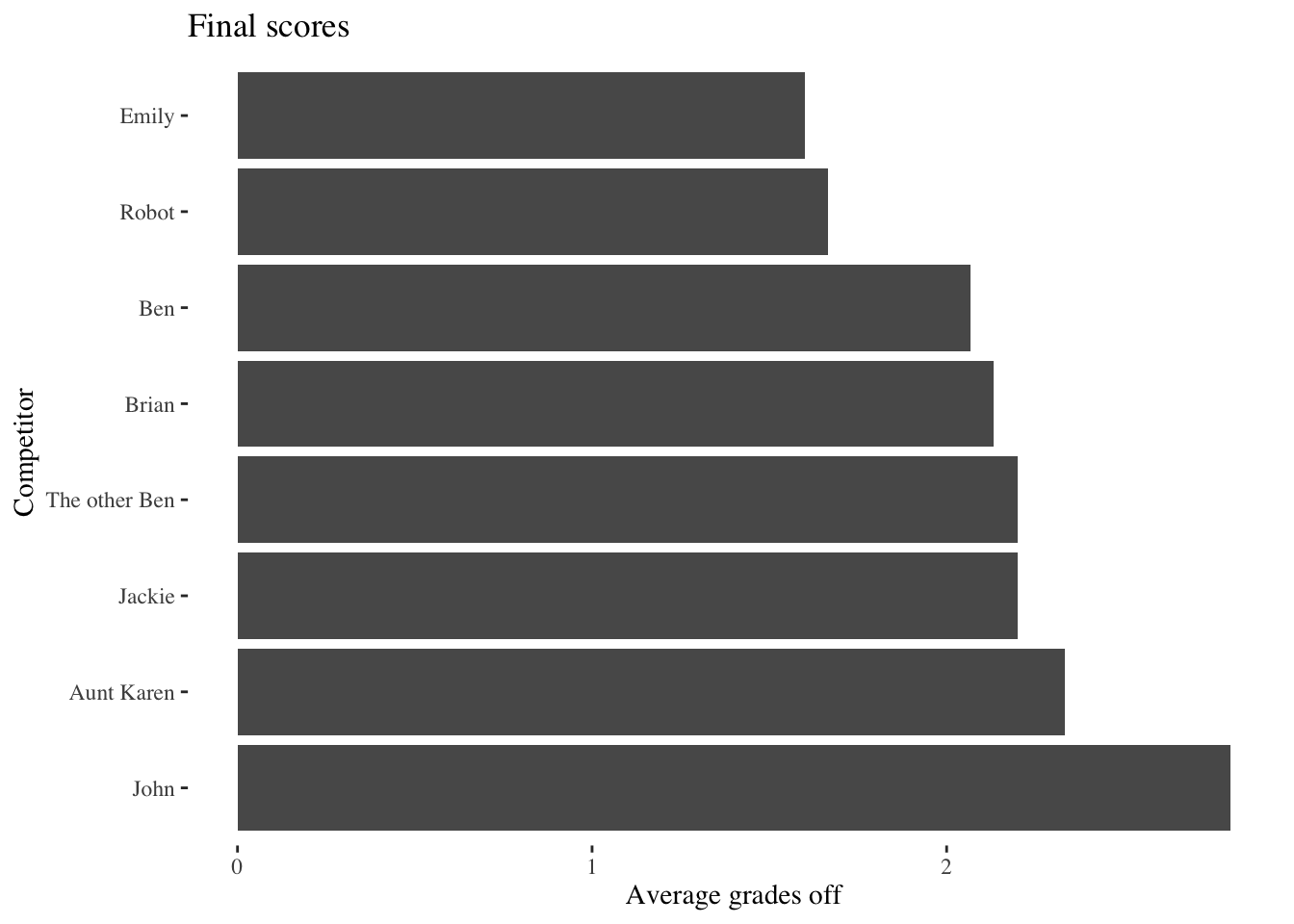
As expected, Emily wins, pulling off a tight victory over the robot in second place.
Wait, who’s the robot?
Okay, I should come clean. I also entered the guess-off, but with a twist: Instead of trying to guess the grades myself, I used the other sixty thousand poems provided in the dataset to build an algorithm that would guess the grade for me. To put it another way: You give the robot a poem, it will estimate the grade of the poem’s author.
(For you data nerds out there, the algorithm is a fairly standard support vector machine built off of a TF-IDF matrix. I played around with some more in-depth models and preprocessing, but, for the most part, the standard SVM performed best)
While the robot couldn’t quite take Emily down, it gave her a run for her money. Let’s take a look at how the robot guessed:
The robot consistently guessed the right answer within 1-2 grades, albeit with a few larger misses, like on “My Bike”. 2
If you are a Skeptical Sally who thinks the robot cheated…
I can assure you - the robot did not read these poems beforehand! It “learned” on all the other poems and had never seen this set of thirty before making its guesses.
The robot did not cheat. But it did do something sneaky.
If you examine the robot’s guesses closely, you might notice something a bit strange: It made guesses in a fairly narrow range. In other words, the robot never guessed below third grade or above eighth grade. In order to understand why it did this - and why that strategy worked - it is important to think more carefully about where these poems came from.
Hipson and Mohammad subtly speak to this in their original paper when they discuss the origin of this dataset. Specifically, they write3:
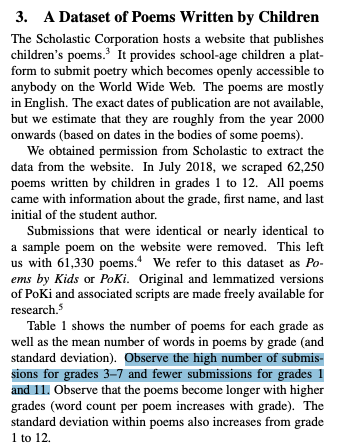
That one highlighted line is short but extremely telling. Because of the way the data was collected (poems self-submitted to Scholastic), most of the poems within the set of sixty thousand were written by third through seventh graders. Makes sense. First and second graders are a bit young to be posting poems, and high schoolers are probably too cool for school.
We can see this pattern directly in the data:
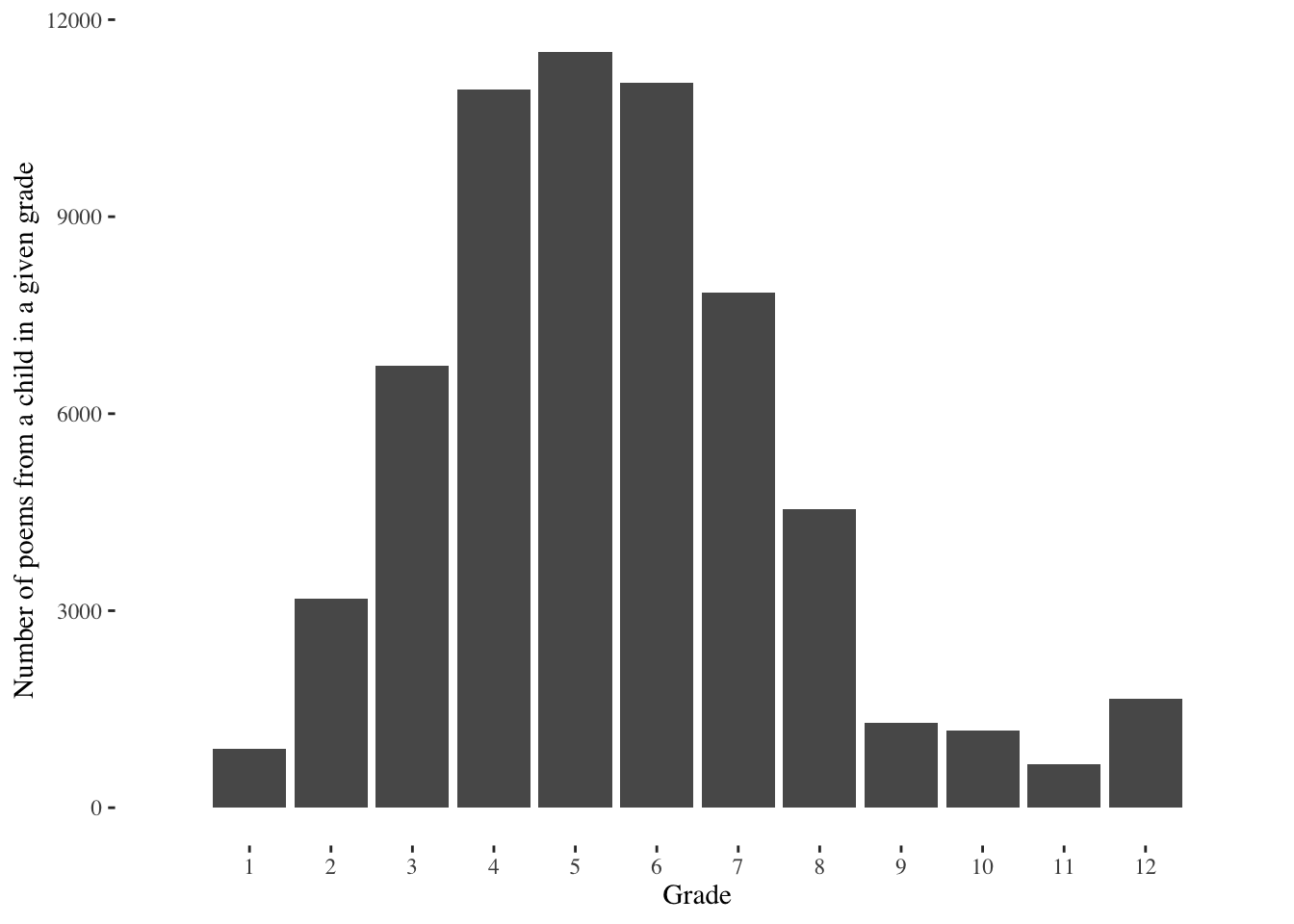
Fifth-graders contributed nearly twelve thousand of the sixty thousand poems, while there were so few poems written by first-graders (~900) that they barely register on the chart.
What does this mean? Well, if we are playing “Guess the Grade” on a sample from this dataset, then guessing “first grade” or one of the high-school grades is somewhat of a fool’s errand. There are so few poems from that group that it is highly unlikely you will get it right. Take a stab at late elementary school or early middle-school, however, and you give yourself the best chance to win. This is what the robot figured out.
Is that fair? Maybe not. What this suggests is that this particular robot will do a good job guessing the grade when given a poem from this set, but if you just ask a random kid off the street to write you a poem 4, the robot’s guesses might not be so hot.
There are actually ways to adjust for this in building the algorithm. This kind of problem - where certain categories in the data appear way more often than others - happens from time to time. I played around with some of these methods (for the data nerds, one of the simpler solutions is to boostrap oversample the less frequent classes), but naturally there were tradeoffs: If the robot is better suited towards getting the “poem from the random street kid” right, it will likely do worse on the Scholastic set used above, because it is doing less to game the system. So I left well enough alone, as I wanted to make sure to give the robot the best shot it could have at beating Emily.
Even the sneakiest of robots, however, clearly cannot beat a trained professional. Emily is the undisputed champ.